就是要摸鱼

最小生成树

发表于 更新于 分类于
本文字数： 6.2k 阅读时长 ≈ 9 分钟
最小生成树的两种方法--Kruskal和Prim

最小生成树

最小生成树仅仅针对无向图

是否成环

参考链接
这里直接用carl给的模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构

// 并查集初始化
void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}
// 并查集里寻根的过程
int find(int u) {
    return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}

// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

// 将v->u 这条边加入并查集
void join(int u, int v) {
    u = find(u); // 寻找u的根
    v = find(v); // 寻找v的根
    if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
    father[v] = u;
}

通过模板，我们可以知道，并查集主要有三个功能。

  1. 寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
  2. 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
  3. 判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点

一个误区

1
2
3
4
5
6
7
8
9
10
11
12
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

// 将v->u 这条边加入并查集
void join(int u, int v) {
    if (isSame) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
    father[v] = u;
}

这里不能直接将isSame抽象出来，在join里面调用，必须寻根以后再father[v] = u;

寻根以后的u v 和 join传入的参数u v 是不一样的！！！

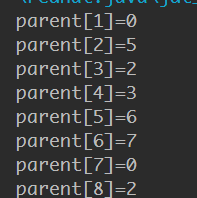
并查集只能判断无向图是否成环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public class test4 {

    public static int n;
    public static int[] father;

    public void init() {
        father = new int[n];
        for (int i = 0; i < n; i++) {
            father[i] = i;
        }
    }

    public int find(int u) {
        if (u == father[u]) {
            return u;
        } else
            return father[u] = find(father[u]);
    }

    public boolean isSame(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

    public void join(int u, int v) {
        u = find(u);
        v = find(v);
        if (u == v)
            return;
        father[v] = u;
    }

    public static void main(String[] args) {
        test4 t = new test4();
        test4.n = 4;
        t.init();

        t.join(1, 2);
        t.join(2, 3);
        t.join(1, 3);

        System.out.println(Arrays.toString(father));
        System.out.println(t.isSame(1, 3));
    }
}

通过这个例子可以看到，t.join(1, 3);还是t.join(3, 1); 最后判断t.isSame(1, 3)都会是true

最小生成树参考视频

Kruskal

Kruskal.java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
import java.util.*;

class Edge implements Comparable<Edge> {
    int from, to, weight;

    public Edge(int from, int to, int weight) {
        this.from = from;
        this.to = to;
        this.weight = weight;
    }

    @Override
    public int compareTo(Edge other) {
        return this.weight - other.weight;
    }
}

public class Kruskal {
    public static int find(int[] parent, int u) {
        if (u == parent[u]) {
            return u;
        }else{
            return parent[u] = find(parent, parent[u]);
        }
    }

    public static void union(int[] parent, int u, int v) {
        u = find(parent, u);
        v = find(parent, v);
        if(u==v) return;
        parent[u] = v;
    }

    public static List<Edge> kruskalMST(List<Edge> edges, int n) {
        Collections.sort(edges);

        int[] parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
		// 最小生成树的边
        List<Edge> result = new ArrayList<>();
        for (Edge edge : edges) {
            int u = find(parent, edge.from);
            int v = find(parent, edge.to);
            // 成环了就跳过
            if (u != v) {
                result.add(edge);
                union(parent, u, v);
            }
        }

        return result;
    }

    public static void main(String[] args) {
        // n 代表顶点的个数
        int n = 4;
        List<Edge> edges = new ArrayList<>();
        edges.add(new Edge(0, 1, 10));
        edges.add(new Edge(0, 2, 6));
        edges.add(new Edge(0, 3, 5));
        edges.add(new Edge(1, 3, 15));
        edges.add(new Edge(2, 3, 4));

        List<Edge> mst = kruskalMST(edges, n);

        for (Edge edge : mst) {
            System.out.println(edge.from + " - " + edge.to + ": " + edge.weight);
        }
    }
}

结果

Prim

普通写法

Prim.java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
public class Prim {
    public static void main(String[] args) {
        // int[][] graph = {
        // {0, 2, 0, 6, 0},
        // {2, 0, 3, 8, 5},
        // {0, 3, 0, 0, 7},
        // {6, 8, 0, 0, 9},
        // {0, 5, 7, 9, 0}
        // };
        int[][] graph = {
                { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
                { 4, 0, 8, 0, 0, 0, 0, 11, 0 },
                { 0, 8, 0, 7, 0, 4, 0, 0, 2 },
                { 0, 0, 7, 0, 9, 14, 0, 0, 0 },
                { 0, 0, 0, 9, 0, 10, 0, 0, 0 },
                { 0, 0, 4, 14, 10, 0, 2, 0, 0 },
                { 0, 0, 0, 0, 0, 2, 0, 1, 6 },
                { 8, 11, 0, 0, 0, 0, 1, 0, 7 },
                { 0, 0, 2, 0, 0, 0, 6, 7, 0 },
        };

        int[] parent = prim(graph);

        // 打印最小生成树的边
        for (int i = 1; i < parent.length; i++) {
            System.out.println("parent["+i+"]="+parent[i] );
        }
    }

    public static int[] prim(int[][] graph) {
        int n = graph.length;
        boolean[] visited = new boolean[n];
        int[] parent = new int[n];
        int[] key = new int[n];

        // 初始化距离数组和父节点数组
        for (int i = 0; i < n; i++) {
            key[i] = Integer.MAX_VALUE;
            parent[i] = -1;
        }
        key[0] = 0;

        // Prim 算法
        for (int i = 0; i < n; i++) {
            int u = -1;
            // 这个for是为了找出当前最近的节点，并标记为已访问
            for (int j = 0; j < n; j++) {
                if (!visited[j] && (u == -1 || key[j] < key[u])) {
                    u = j;
                }
            }

            visited[u] = true;

            // 这个for是为了看那些没有被访问过的节点，更新他们的距离
            for (int v = 0; v < n; v++) {
                if (!visited[v] && graph[u][v] != 0 && graph[u][v] < key[v]) {
                    key[v] = graph[u][v];
                    parent[v] = u;
                }
            }
        }

        return parent;
    }
}

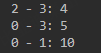
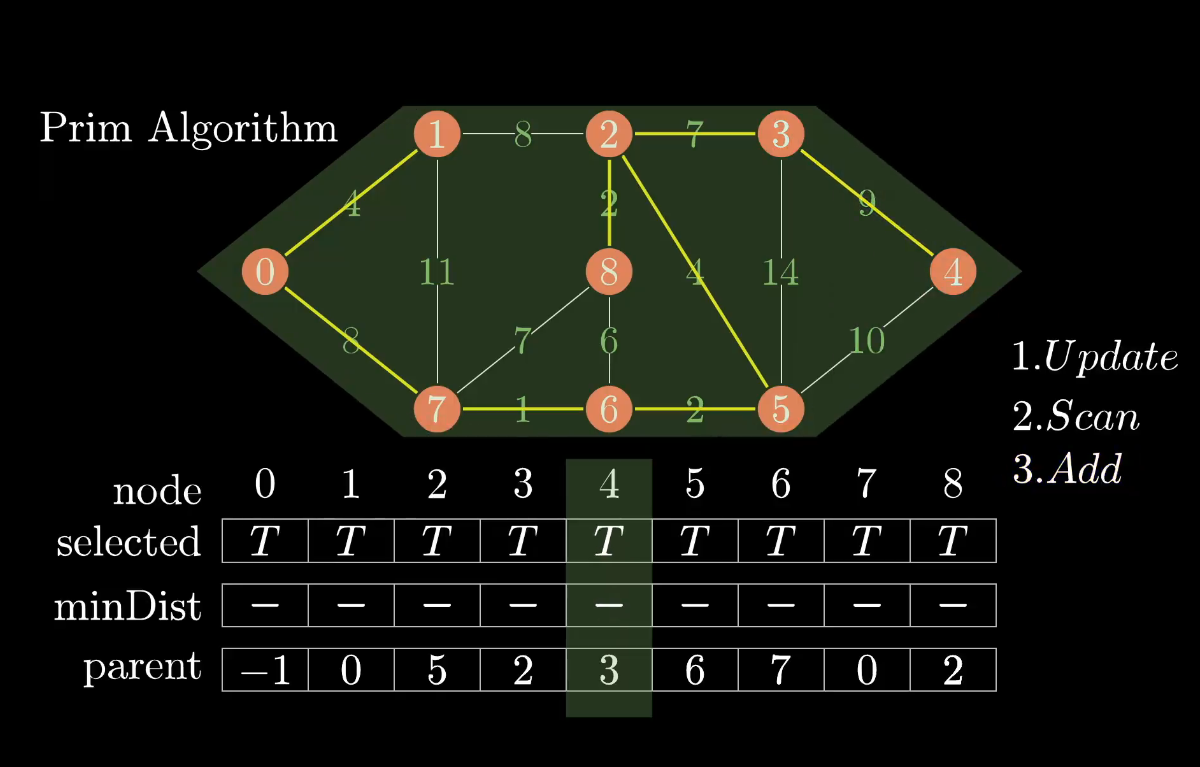
最小生成树的结果不唯一

上述代码的运行结果为

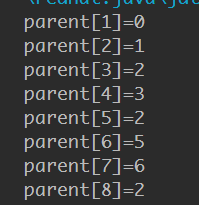
另外一种树为，权值和均为37

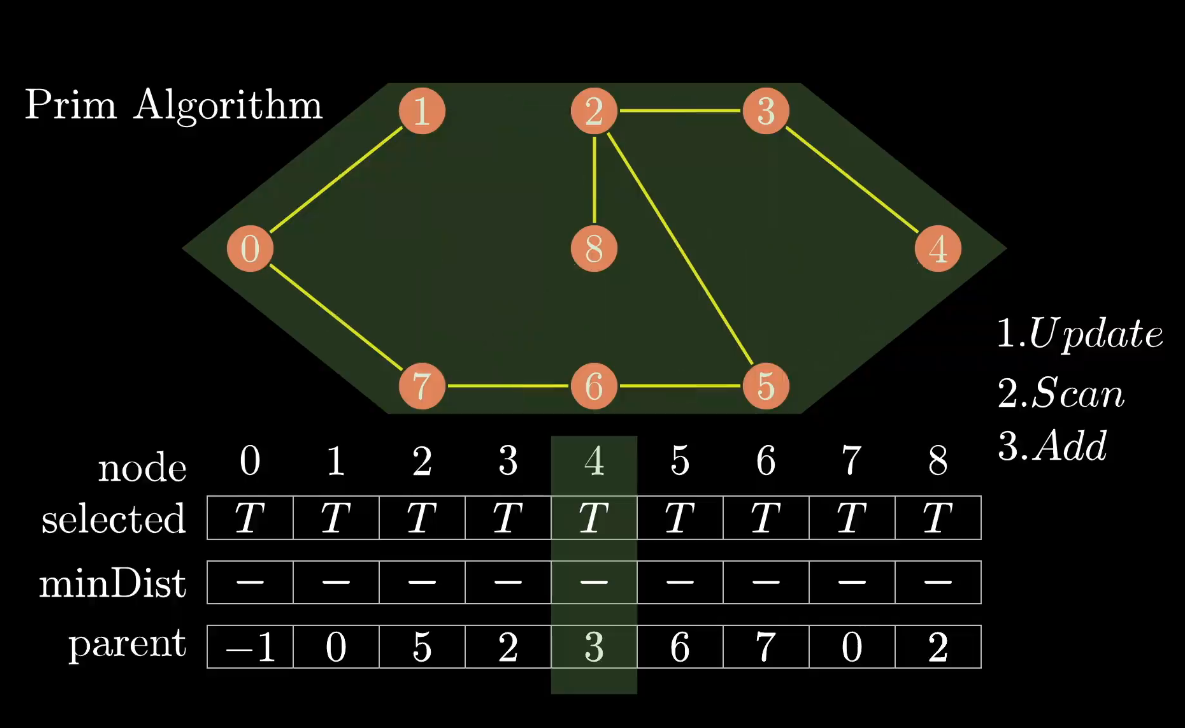
优先级队列的写法

Prim2.java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import java.util.PriorityQueue;

public class Prim2 {
    public static void main(String[] args) {
        int[][] graph = {
                { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
                { 4, 0, 8, 0, 0, 0, 0, 11, 0 },
                { 0, 8, 0, 7, 0, 4, 0, 0, 2 },
                { 0, 0, 7, 0, 9, 14, 0, 0, 0 },
                { 0, 0, 0, 9, 0, 10, 0, 0, 0 },
                { 0, 0, 4, 14, 10, 0, 2, 0, 0 },
                { 0, 0, 0, 0, 0, 2, 0, 1, 6 },
                { 8, 11, 0, 0, 0, 0, 1, 0, 7 },
                { 0, 0, 2, 0, 0, 0, 6, 7, 0 },
        };

        int[] parent = prim(graph);

        // 打印最小生成树的边
        for (int i = 1; i < parent.length; i++) {
            System.out.println("parent[" + i + "]=" + parent[i]);
        }
    }

    public static int[] prim(int[][] graph) {
        int n = graph.length;
        boolean[] visited = new boolean[n];
        int[] parent = new int[n];
        int[] key = new int[n];

        // 初始化距离数组和父节点数组
        for (int i = 0; i < n; i++) {
            key[i] = Integer.MAX_VALUE;
            parent[i] = -1;
        }
        key[0] = 0;

        // 使用优先队列存储待处理的顶点
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        for (int i = 0; i < n; i++) {
            pq.offer(new int[] { key[i], i });
        }

        // Prim 算法
        while (!pq.isEmpty()) {
            int[] minNode = pq.poll();
            int u = minNode[1];
            visited[u] = true;

            for (int v = 0; v < n; v++) {
                if (!visited[v] && graph[u][v] != 0 && graph[u][v] < key[v]) {
                    key[v] = graph[u][v];
                    parent[v] = u;
                    pq.offer(new int[] { key[v], v });
                }
            }
        }

        return parent;
    }
}

优先级队列的思想还是比较容易理解的，刚好其输出是另外一颗最小树，也刚好验证了上面的说法