具体原理可以参考最完整+全解析的Floyd算法(C++版) 视频讲解
python实现如下1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68# dist是任意两点之间的最短路径，path是这两点之间的最短路径，所需途径的点
def floyd_warshall(graph):
n = len(graph)
dist = [[float('inf')] * n for _ in range(n)]
path = [[-1] * n for _ in range(n)]
# 初始化距离矩阵和路径矩阵
for i in range(n):
for j in range(n):
if i == j:
dist[i][j] = 0
elif graph[i][j] != 0:
dist[i][j] = graph[i][j]
elif graph[i][j] == 0 and i!=j:
dist[i][j] = float('inf')
# Floyd-Warshall 算法
for k in range(n):
for i in range(n):
for j in range(n):
if dist[i][k] != float('inf') and dist[k][j] != float('inf'):
new_dist = dist[i][k] + dist[k][j]
if new_dist < dist[i][j]:
dist[i][j] = new_dist
path[i][j] = k
return dist, path
# 示例图
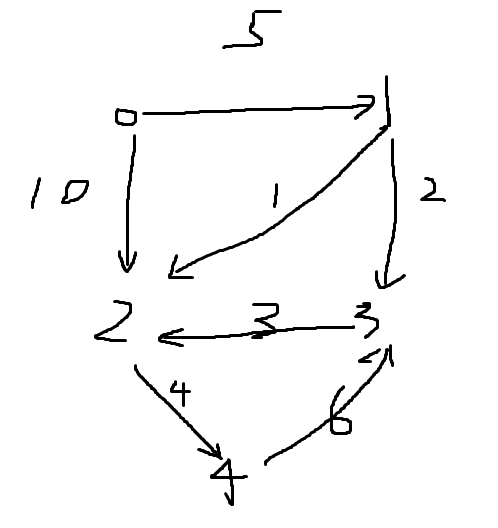
graph = [[0, 5, 10, 0, 0],
[0, 0, 1, 2, 0],
[0, 0, 0, 0, 4],
[0, 0, 3, 0, 0],
[0, 0, 0, 6, 0]]
dist, path = floyd_warshall(graph)
print(f"dist={dist},\npath = {path},\ngraph={graph}\n")
# 打印距离矩阵
print("Distances:")
for row in dist:
print(row)
# 打印路径矩阵
print("\nPaths:")
for row in path:
print(row)
# 打印顶点对之间的最短路径
def print_shortest_path(src, dest, path):
if path[src][dest] == -1:
if dist[src][dest] != float('inf'):
print(src, end=" -> ")
print(dest)
else:
print(f"src不可达dest！！！")
else:
mid = path[src][dest]
print_shortest_path(src,mid,path)
print_shortest_path(mid,dest,path)
# # 示例：打印顶点 0 到顶点 4 的最短路径
print("\npath:")
print_shortest_path(1, 4, path)
graph如下图所示
运行结果
