【王树森】深度强化学习(DRL)_哔哩哔哩_bilibili
深度强化学习
1、RL术语
X是随机变量,x是观测值
state s
Action a,a是agent做的,以马里奥为例,left right up
policy
reward 以马里奥为例,捡到金币+1,赢了+1w,输了扣1w
state transition 状态转移
强化学习中两个随机性来源:动作的随机性,状态转移的随机。随机产生a,随机产生s
trajectory:每一步是
Return: cumulative future reward
Acition-Value Function for policy
Optimal action-value function Q最大的时候
State-Value function
总结就是,动作价值函数是状态
强化学习任务,一是学习策略函数,二是学习Q函数。学习两者之一即可。
value-based learning: DQN,任务是最大化Q 用到temporal different TD算法
Policy-based learning :任务是最大化
Actor-critic method: policy network + value network
2、Value-Based RL
用一个神经网络去近似
如果我们知道了
但是我们现在没有
但是怎么训练?用TD训练,目的是让TD error越小越好
类比driving time例子,TD公式一般类似于这样,左边是T时刻的估计,右边是TD target,包含一个真实值和T+1时刻的估计
而在强化学习中
注意到这里,为什么要求一个max?我的理解是,因为我们的目标就是训练一个最优的Q?
怎么训呢?


3、Policy-Based RL
策略函数
如果状态有限,直接用一个表记录就行,超级马里奥需要用函数去近似
回顾一下状态价值函数
通过神经网络去近似策略函数
Policy-based learning:Learn
那么算policy gradient的时候,需要用到梯度上升,不严谨的推导可以得到两个公式,分别对应离散和连续
这里策略函数很复杂,积分求不出来,只能用MC去近似期望,MC就是抽一个或很多个样本,去近似期望

步骤如下

但问题是第三步中的Q咋算的?有两种方式


4、Actor-Critic methods
结合了价值学习和策略学习



总结一下算法步骤,还有一个值得注意的点是,第九步中用
前者是标准算法,后者被称为Policy Gradient with baseline,收敛的更快


5、AlphaGo
蒙特卡洛 Monte Carlo
第一个例子是均匀抽样估算Pi值
第二个例子是Buffon’s Needle Problem估算Pi值
第三个例子是求阴影面积
第四个例子是Monte Carlo求Pi
Monte Carlo可能是错的,但是离真实值很接近,我们不需要那么精确,在机器学习中够用了。
Random Permutation和 Fisher-Yates
推导待续
TD Learning
DQN高级技巧
大幅提升DQN的表现
回顾一下DQN,是学习一个Q star函数
1、Expeirence Replay 经验回放

两个好处:1.打破了序列的相关性 2.可以重复利用经验
2、Prioritized Expeirence Replay 优先经验回访
用非均匀抽样代替均匀抽样:用TD error去给经验值打一个权重,因为越少见的场景,TD error越大,这样的经验是比较重要的
两种抽样方式


2、DQN高估问题 Bootstrapping

两个高估来源

总结来说就是,DQN估计
均匀高估和非均匀高估,而均匀高估其实是无所谓的。

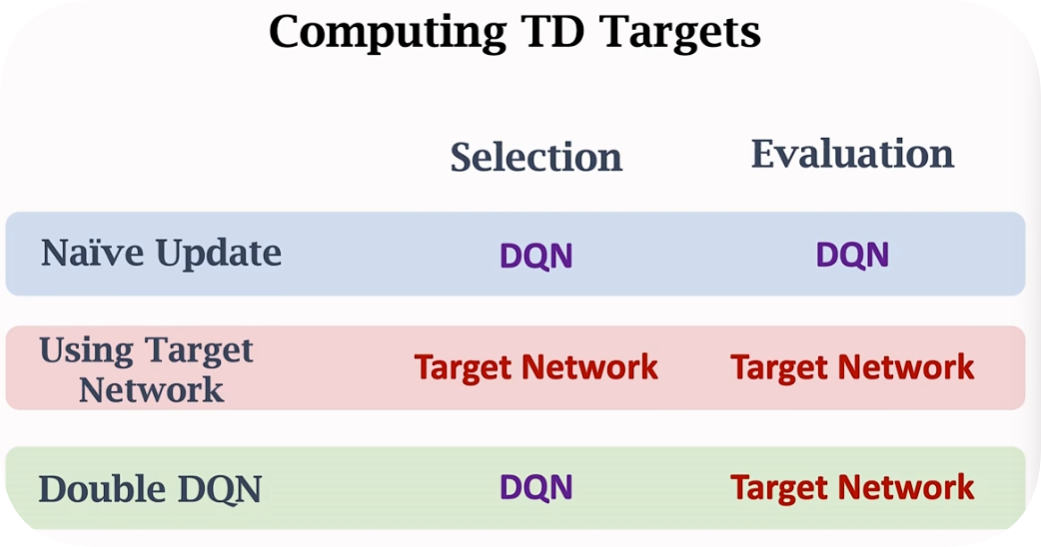
解决方法也有两种,分别是target network和double DQN

本质上都是再用一个新的netwrok去解决高估问题。区别就在于求TD Target的时候,更新参数的时候,有一些区别,细节如下。
3、Dueling Network


回顾一下
其实到这里就能够理解了,一个是单次动作得到的回报,一个是平均回报
然后假设已知了最优的策略函数,由此引申出优势函数的定义,其中


Dueling Network定义

对网络结构的改进
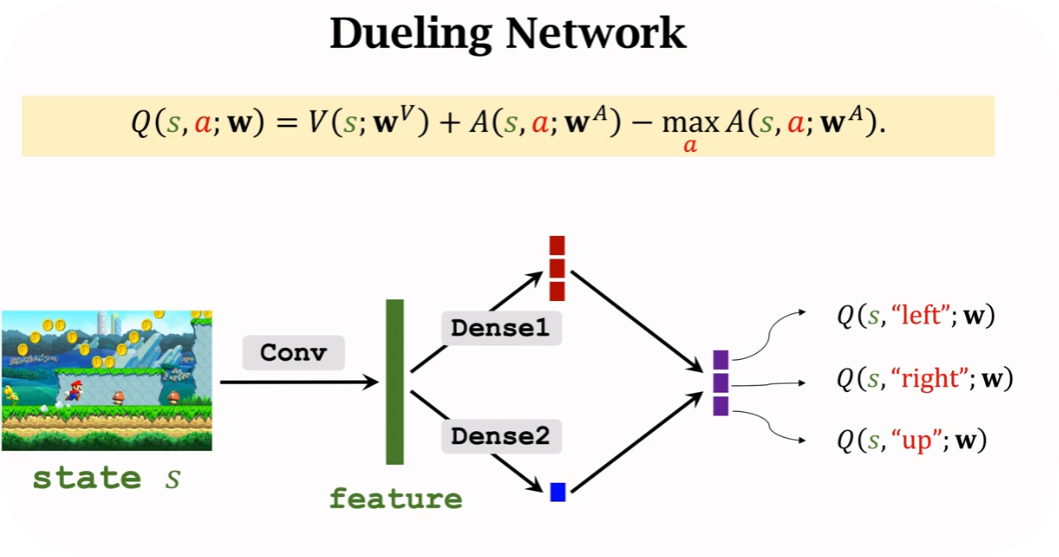
根因是解决不唯一性,为了保证两个网络训练更稳定,实际使用中一般用mean而不用max,因为mean效果更好



策略梯度中的baseline
1、Policy Gradient with Baseline
目的:引入baseline,降低方差,收敛更快
复习一下

baseline的性质
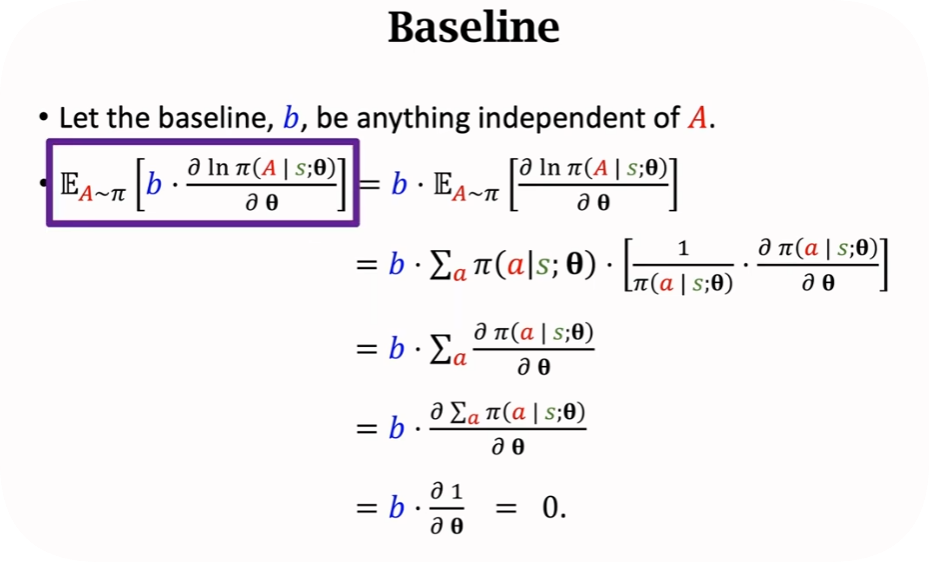

公式里面有期望,求起来会比较困难,实际使用过程中,会使用蒙特卡洛近似。


实际上使用的时候,都是用
b的两种选择方式


2、REINFORCE with Baseline
总结就是三次近似

两次蒙特卡洛近似,因为是无偏估计。
还一次神经网络近似。

两个网络:一个策略网路,一个价值网络
怎么更新呢?

3、Advantage Actor-Critic(A2C)

怎么训练的?

理论证明暂略。。。
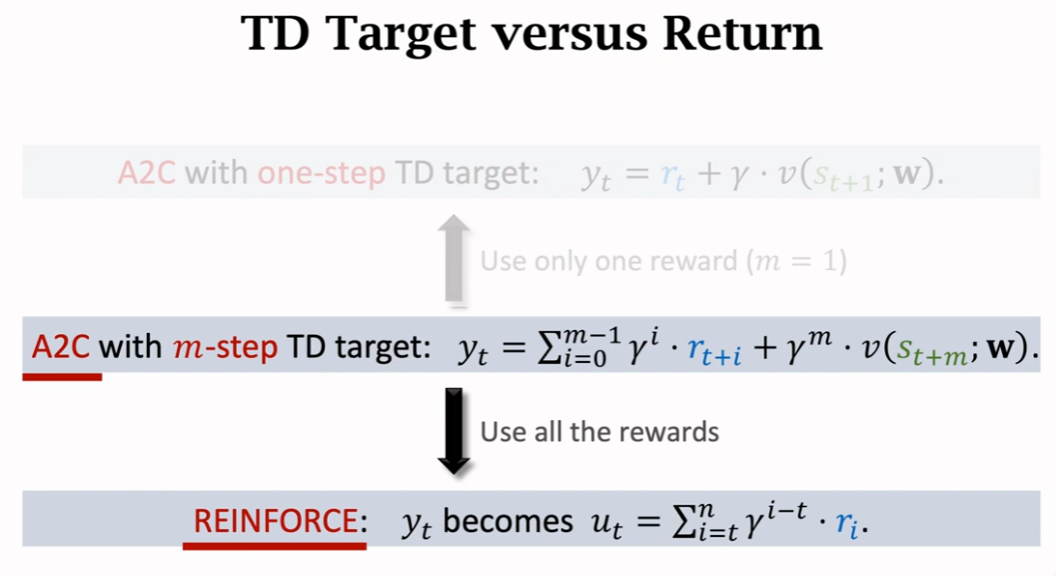
4、REINFORCE with Baseline和A2C的异同
其实从上面5和6就能看出来区别,求TD target的时候,不一样
前者是完全基于观测,而A2C一部分是观测,一部分是网路的估计。
A2C和REINFORCE是相互特例